Portal talk:Mathematics/Archive2020

Duplicate "Did you know"

Number 34 and Number 43 in “Did you know” of Mathematics Portal are the same. — Preceding unsigned comment added by AshrithSagar (talk • contribs) 08:22, 5 June 2020 (UTC)

I have replaced #43. - dcljr (talk) 09:42, 7 June 2020 (UTC)

WP:RECOG discussion

dcljr, what do you think about automating the "Selected article" section using {{Transclude list item excerpts as random slideshow}}? This can be done after JL-Bot populates the section #Recognized content above. For an example of how it works, see Portal:Sports and its list of articles populated by the bot. —⁠andrybak (talk) 18:14, 8 June 2020 (UTC)

Have not had a chance to look into this. Hang on… - dcljr (talk) 07:22, 10 June 2020 (UTC)

Dcljr, JL-Bot has updated the section above. 48 featured and good articles in total. Perhaps, more templates and categories could be added to the current list, which I made from Wikipedia:WikiProject_Council/Directory/Science#Mathematics. —⁠andrybak (talk) 16:38, 18 June 2020 (UTC)

The bot output has been moved to Portal:Mathematics/Recognized content. —⁠andrybak (talk) 15:12, 5 November 2020 (UTC)

Here's a demo of how this would look like:

• 

  

  In this example, the alternating sum of angles (clockwise from the bottom) is 90° − 45° + 22.5° − 22.5° + 45° − 90° + 22.5° − 22.5° = 0°. Since it adds to zero, the crease pattern may be flat-folded.

  
  Kawasaki's theorem or Kawasaki–Justin theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that may be folded to form a flat figure. It states that the pattern is flat-foldable if and only if alternatingly adding and subtracting the angles of consecutive folds around the vertex gives an alternating sum of zero.
  Crease patterns with more than one vertex do not obey such a simple criterion, and are NP-hard to fold.
  
  The theorem is named after one of its discoverers, Toshikazu Kawasaki. However, several others also contributed to its discovery, and it is sometimes called the Kawasaki–Justin theorem or Husimi's theorem after other contributors, Jacques Justin and Kôdi Husimi. (Full article...)
• 

  

  Geometric visualization of the $X+Y$ sorting problem. The input sets $X$ and $Y$ are represented by the sets of vertical and horizontal black lines (respectively), and the goal of the problem is to sort the crossing points by the positions of the red diagonal lines through them.

  
  In computer science, ${\boldsymbol {X}}+{\boldsymbol {Y}}$ sorting is the problem of sorting pairs of numbers by their sums. Applications of the problem include transit fare minimisation, VLSI design, and sparse polynomial multiplication. As with comparison sorting and integer sorting more generally, algorithms for this problem can be based only on comparisons of these sums, or on other operations that work only when the inputs are small integers.
  
  It is unknown whether this problem has a comparison-based solution whose running time is asymptotically faster than sorting an unstructured list of equally many items. Therefore, research on the problem has focused on two approaches to settle the question of whether such an improvement is possible: the development of algorithms that improve on unstructured sorting in their number of comparisons rather than in their total running time, and lower bounds for the number of comparisons based on counting cells in subdivisions of high-dimensional spaces. Both approaches are historically tied together, in that the first algorithms that used few comparisons were based on the weakness of the cell-counting lower bounds. (Full article...)
• 

  

  A perspective projection of a dodecahedral tessellation in H³. Note the recursive structure: each pentagon contains smaller pentagons, which contain smaller pentagons. This is an example of a subdivision rule arising from a finite universe (i.e. a closed 3-manifold).

  
  
  In mathematics, a finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. Subdivision rules in a sense are generalizations of regular geometric fractals. Instead of repeating exactly the same design over and over, they have slight variations in each stage, allowing a richer structure while maintaining the elegant style of fractals. Subdivision rules have been used in architecture, biology, and computer science, as well as in the study of hyperbolic manifolds. Substitution tilings are a well-studied type of subdivision rule. (Full article...)
• 
  The Math Myth: And Other STEM Delusions is a 2016 nonfiction book by Queens College political scientist Andrew Hacker analyzing and critiquing the United States educational system's teaching of mathematics as a linear progression towards more advanced fields. Based on a 2012 New York Times op-ed by Hacker titled "Is Algebra Necessary", Hacker argues that the teaching of advanced algebra, trigonometry, and calculus is not useful to the majority of students. He further claims that the requirement of advanced mathematics courses in secondary education contributes to dropout rates and impedes socioeconomically disadvantaged students from pursuing further education. Hacker critiques the Common Core system and American focus on STEM education in lieu of social sciences, arguing that the educational system should prioritize "numeracy" over pure mathematics education.
  
  The Math Myth received broadly critical coverage from critics and mathematicians, some citing Hacker's arguments as "disingenuous" and contributing to an elitist attitude towards mathematics, with many citing a lack of exploration on mathematics in early childhood and primary education. Others praised Hacker's work, describing the book as offering a convincing critique of STEM education in the United States and empowering to students struggling in mathematics. (Full article...)
• 
  In the mathematical fields of graph theory and finite model theory, the logic of graphs deals with formal specifications of graph properties using sentences of mathematical logic. There are several variations in the types of logical operation that can be used in these sentences. The first-order logic of graphs concerns sentences in which the variables and predicates concern individual vertices and edges of a graph, while monadic second-order graph logic allows quantification over sets of vertices or edges. Logics based on least fixed point operators allow more general predicates over tuples of vertices, but these predicates can only be constructed through fixed-point operators, restricting their power.
  
  A sentence $S$ may be true for some graphs, and false for others; a graph $G$ is said to model $S$, written $G\models S$, if $S$ is true of the vertices and adjacency relation of $G$. The algorithmic problem of model checking concerns testing whether a given graph models a given sentence. The algorithmic problem of satisfiability concerns testing whether there exists a graph that models a given sentence.
  Although both model checking and satisfiability are hard in general, several major algorithmic meta-theorems show that properties expressed in this way can be tested efficiently for important classes of graphs. (Full article...)
• 

  

  3 + 2 = 5 with apples, a popular choice in textbooks

  
  
  Addition (usually signified by the plus symbol +) is one of the four basic operations of arithmetic, the other three being subtraction, multiplication and division. The addition of two whole numbers results in the total amount or sum of those values combined. The example in the adjacent image shows two columns of three apples and two apples each, totaling at five apples. This observation is equivalent to the mathematical expression "3 + 2 = 5" (that is, "3 plus 2 is equal to 5").
  
  Besides counting items, addition can also be defined and executed without referring to concrete objects, using abstractions called numbers instead, such as integers, real numbers and complex numbers. Addition belongs to arithmetic, a branch of mathematics. In algebra, another area of mathematics, addition can also be performed on abstract objects such as vectors, matrices, subspaces and subgroups. (Full article...)
• 

  

  Wave functions of the electron in a hydrogen atom at different energy levels. Quantum mechanics cannot predict the exact location of a particle in space, only the probability of finding it at different locations. The brighter areas represent a higher probability of finding the electron.

  
  Quantum mechanics is a fundamental theory that describes the behavior of nature at and below the scale of atoms. It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.
  
  Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation, valid at large (macroscopic/microscopic) scale. (Full article...)
• 

  

  Geometric representation of the square pyramidal number 1 + 4 + 9 + 16 = 30.

  
  In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.
  
  As well as counting spheres in a pyramid, these numbers can be described algebraically as a sum of the first $n$ positive square numbers, or as the values of a cubic polynomial. They can be used to solve several other counting problems, including counting squares in a square grid and counting acute triangles formed from the vertices of an odd regular polygon. They equal the sums of consecutive tetrahedral numbers, and are one-fourth of a larger tetrahedral number. The sum of two consecutive square pyramidal numbers is an octahedral number. (Full article...)
• 

  

  
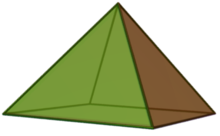
  In geometry, a square pyramid is a pyramid with a square base, having a total of five faces. If the apex of the pyramid is directly above the center of the square, it is a right square pyramid with four isosceles triangles; otherwise, it is an oblique square pyramid. When all of the pyramid's edges are equal in length, its triangles are all equilateral. It is called an equilateral square pyramid, an example of a Johnson solid.
  
  Square pyramids have appeared throughout the history of architecture, with examples being Egyptian pyramids and many other similar buildings. They also occur in chemistry in square pyramidal molecular structures. Square pyramids are often used in the construction of other polyhedra. Many mathematicians in ancient times discovered the formula for the volume of a square pyramid with different approaches. (Full article...)
• 

  

  17 indivisible camels

  
  The 17-animal inheritance puzzle is a mathematical puzzle involving unequal but fair allocation of indivisible goods, usually stated in terms of inheritance of a number of large animals (17 camels, 17 horses, 17 elephants, etc.) which must be divided in some stated proportion among a number of beneficiaries. It is a common example of an apportionment problem.
  
  Despite often being framed as a puzzle, it is more an anecdote about a curious calculation than a problem with a clear mathematical solution. Beyond recreational mathematics and mathematics education, the story has been repeated as a parable with varied metaphorical meanings. (Full article...)
• 
  The Euclid–Euler theorem is a theorem in number theory that relates perfect numbers to Mersenne primes. It states that an even number is perfect if and only if it has the form 2^p−1(2^p − 1), where 2^p − 1 is a prime number. The theorem is named after mathematicians Euclid and Leonhard Euler, who respectively proved the "if" and "only if" aspects of the theorem.
  
  It has been conjectured that there are infinitely many Mersenne primes. Although the truth of this conjecture remains unknown, it is equivalent, by the Euclid–Euler theorem, to the conjecture that there are infinitely many even perfect numbers. However, it is also unknown whether there exists even a single odd perfect number. (Full article...)
• 

  

  
  Rust is a general-purpose programming language emphasizing performance, type safety, and concurrency. It enforces memory safety, meaning that all references point to valid memory. It does so without a traditional garbage collector; instead, memory safety errors and data races are prevented by the "borrow checker", which tracks the object lifetime of references at compile time.
  
  Rust does not enforce a programming paradigm, but was influenced by ideas from functional programming, including immutability, higher-order functions, algebraic data types, and pattern matching. It also supports object-oriented programming via structs, enums, traits, and methods. It is popular for systems programming. (Full article...)
• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.
  
  Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique which opposes all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
• 
  
  

  

  Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

  
  Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
  
  Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
• 
  
  

  

  Rejewski, c. 1932

  
  Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
  
  Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)

—⁠andrybak (talk) 15:14, 5 November 2020 (UTC)

Unfinished selected pictures

dcljr, please see the added captions:

1. Special:Diff/987171957
2. Special:Diff/987172036
3. Special:Diff/987172086
4. Special:Diff/987172114

If that's enough, I'll remove the disclaimer and add these pictures to the rotation on the portal's page. —⁠andrybak (talk) 13:29, 5 November 2020 (UTC)

I did it, thanks. (I still plan to do additional copyediting/expansion of the description text for each, but what's currently there will do for now.) - dcljr (talk) 02:16, 6 November 2020 (UTC)